One to one function

Mathematics being a vast subject and is very interesting to learn. There are unlimited topics which can be studied. Importance of mathematics is given to you in my previous post. The topic i have discussed today is One to One function.

I will explain you the concept one to one function with the help of an example. This will be a very interesting and informative post for you. In my next post i will help you with the relation with functions and to find the product of two functions.

What is a function? It is a set of a set of ordered pairs. They have the same component in the first and a different component in the different place.

A function is said to be One to one function when all the elements of a particular function have at least one element on to the other function. Lets learn that in more details with some examples.

Example No.1

If A= {1, 2, 3, 4} and f: A-->B is function defined by f(x) =x

^2-x+1 then find the range of 'f'

Solution:-

f (1) =1^2-1+1=1

f (2) = 2^2-2+1=3

f(3)=3^2-3+1=7

f(4)=4^2-4+1=13

Hence Range is {1, 3, 7, and 13}

Example No 2:-

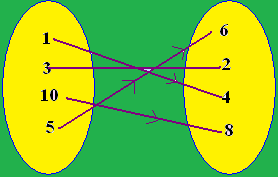
Find whether the following function defined by f = {(3 , 2),(1 , 4),(10 , 8),( 5, 6)} is a one to one function?

Given function can be explained to you in the form of a diagram below.

From the figure we can note that each element have separate output.

Therefore the given function f is a one to one function.

The above mentioned examples will make you understand the concept one to one function easily, look out for more examples from your text books, let me know how much did you learn from this post? :-)